ORIGEM DO CONCEITO DE DERIVADA DE UMA FUNÇÃO
O conceito de função que hoje pode parecer simples, é o resultado de uma lenta e longa evolução histórica iniciada na Antiguidade quando, por exemplo, os matemáticos Babilónios utilizaram tabelas de quadrados e de raízes quadradas e cúbicas ou quando os Pitagóricos tentaram relacionar a altura do som emitido por cordas submetidas à mesma tensão com o seu comprimento. Nesta época o conceito de função não estava claramente definido: as relações entre as variáveis surgiam de forma implícita e eram descritas verbalmente ou por um gráfico.
Só no séc. XVII, quando Descartes e Pierre Fermat introduziram as coordenadas cartesianas, se tornou possível transformar problemas geométricos em problemas algébricos e estudar analiticamente funções. A Matemática recebe assim um grande impulso, nomeadamente na sua aplicabilidade a outras ciências - os cientistas passam, a partir de observações ou experiências realizadas, a procurar determinar a fórmula ou função que relaciona as variáveis em estudo. A partir daqui todo o estudo se desenvolve em torno das propriedades de tais funções. Por outro lado, a introdução de coordenadas, além de facilitar o estudo de curvas já conhecidas permitiu a "criação" de novas curvas, imagens geométricas de funções definidas por relações entre variáveis.
Foi enquanto se dedicava ao estudo de algumas destas
funções que Fermat deu conta das limitações do conceito clássico de recta
tangente a uma curva como sendo aquela que encontrava a curva num único ponto.
Tornou-se assim importante reformular tal conceito e encontrar um processo
de traçar uma tangente a um gráfico num dado ponto - esta dificuldade ficou
conhecida na História da Matemática como o " Problema da Tangente".
Fermat resolveu esta dificuldade de uma maneira muito simples: para determinar
uma tangente a uma curva num ponto P considerou outro ponto Q sobre a curva;
considerou a recta PQ secante à curva. Seguidamente fez deslizar Q ao longo da
curva em direcção a P, obtendo deste modo rectas PQ que se aproximavam duma
recta
t a que Fermat chamou a recta tangente à curva no ponto P.
Fermat notou que para certas funções, nos pontos onde a curva assumia valores extremos, a tangente ao gráfico devia ser uma recta horizontal, já que ao comparar o valor assumido pela função num desses pontos P(x, f(x)) com o valor assumido no outro ponto Q(x+E, f(x+E)) próximo de P, a diferença entre f(x+E) e f(x) era muito pequena, quase nula, quando comparada com o valor de E, diferença das abcissas de Q e P. Assim, o problema de determinar extremos e de determinar tangentes a curvas passam a estar intimamente relacionados.
Estas ideias constituíram o embrião do conceito de DERIVADA e levou Laplace a considerar Fermat "o verdadeiro inventor do Cálculo Diferencial". Contudo, Fermat não dispunha de notação apropriada e o conceito de limite não estava ainda claramente definido.
No séc.XVII, Leibniz algebriza o Cálculo Infinitésimal, introduzindo os conceitos de variável, constante e parâmetro, bem como a notação dx e dy para designar "a menor possível das diferenças em x e em y. Desta notação surge o nome do ramo da Matemática conhecido hoje como " Cálculo Diferencial ".
Assim, embora só no século XIX Cauchy introduzia formalmente o conceito de limite e o conceito de derivada, a partir do séc. XVII, com Leibniz e Newton, o Cálculo Diferencial torna-se um instrumento cada vez mais indispensável pela sua aplicabilidade aos mais diversos campos da Ciência.
Derivadas
|
A derivada de uma função
y = f(x) num ponto x = x0
, é igual ao valor da tangente trigonométrica do ângulo formado pela
tangente geométrica à curva representativa de |
A derivada de uma função
y = f(x), pode ser representada também pelos
símbolos:
y' , dy/dx
ou f ' (x).
A derivada de uma função f(x) no ponto x0 é dada por:
![]()
Algumas derivadas básicas
Nas fórmulas
abaixo, u e v são funções da variável x.
Sendo
a, b, c e n são constantes.
Derivada de uma constante
![]()
Derivada da potência
![]()
Portanto:
![]()
Soma / Subtração
![]()
Produto por uma constante
![]()
Derivada do produto
![]()
Derivada da divisão
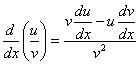
Potência de uma função
![]()
Derivada de uma função composta
![]()
Derivadas
A fórmula:
![]()
é
conhecida como regra da cadeia. Ela pode ser
escrita como:
![]()
Outra fórmula
similar é a seguinte:
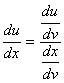
A inversa da função y(x) é a função x(y):
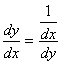
Derivadas de funções trigonométricas e suas inversas
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
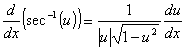
![]()
Derivadas de funções exponencial e logarítmica
Derivada do logaritmo natural
![]()
Derivada do logaritmo
em outras bases
![]()
Exponencial
![]()
![]()
![]()
Lembre-se da
definição da função logarítmica com base a > 0:
![]()
Derivadas das funções hiperbólicas e suas inversas
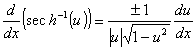
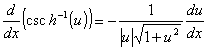
Lembre-se das definições das funções trigonométricas:
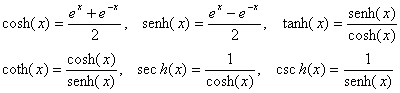
Derivadas de alta ordem
Seja y = f(x). Temos:
A segunda derivada é dada por:
![]()
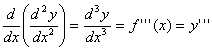
A enésima derivada é dada por:
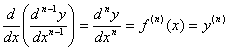
Em alguns
livros, a seguinte notação também é usada:
![]()