Considera tijolos do tipo 2x1 (isto é, cujas medidas dos lados são respetivamente 1 e 2 unidades).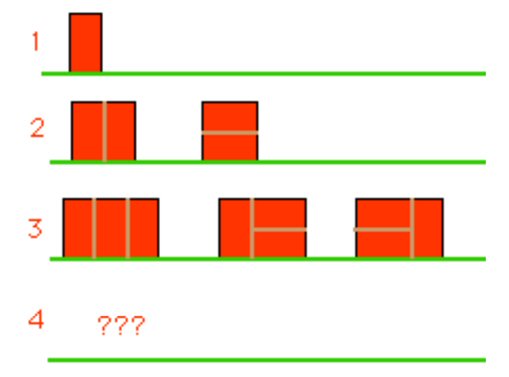

Se quiseres construir uma parede de tijolos com duas unidades de altura, podes fazê-lo num número diverso de formas, dependendo do comprimento da parede.

Por exemplo, existe apenas uma forma de parede com o comprimento 1,  pondo o tijolo em pé.

Existem duas formas de construir uma parede de comprimento 2. A primeira forma é colocá-los lateralmente um no topo do outro. A segunda é colocá-los longitudinalmente junto um do outro.

Existem três formas de construção para paredes de comprimento 3 (como ilustra a figura anterior).

Quantas formas diferentes se consegue encontrar para uma parede de comprimento 4? E  de comprimento 5?

Repara  para o número de formas que encontraste, para uma parede de comprimento 1, 2, 3, 4 e 5.

Será que consegues descobrir alguma coisa que seja familiar em todos estes casos?

Sugestão: Designa por F(n) "o número de formas de construir paredes de altura 2 e comprimento n" e tenta justificar como é que os números de Fibonacci respondem a este problema.