Teresa Dias
Departamento de Matemática
CONJUNTO DE CANTOR
Seja I
= [0, 1] e definamos a sucessão
de subconjuntos encaixados,
fechados e limitados de [0, 1] do
seguinte modo: para obter
L1,
retire-se do intervalo I o seu
terço médio
]1/3, 2/3[;
L2
é obtido de
L1
removendo-se dele os terços médios
]1/9,
2/9[ e ]7/9, 8/9[; em geral,
Ln+1
resulta de se retirar de
Ln
os terços médios abertos de cada um dos 2n
intervalos fechados que constituem
Ln.
Repetindo o processo indutivamente, obtemos um subconjunto fechado do intervalo
[0, 1], o Conjunto
ternário de Cantor C,
que é a intersecção
.
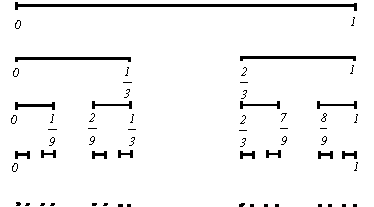
Note-se que a amplitude cada um dos 2n intervalos, que constituem Ln, é igual a
e que a soma dos comprimentos dos intervalos abertos, removidos na construção de C, é igual a um, exactamente o comprimento do intervalo inicial I. De facto, designando por Lnc o conjunto dos intervalos abertos removidos na n-ésima etapa da construção de C, temos que o comprimento de L1c é 1/3 , o comprimento de L2c é 2/9 e, em geral, o comprimento de Lnc é
Assim, a soma dos comprimentos de todos os intervalos abertos removidos na
construção do conjunto ternário de Cantor é igual a
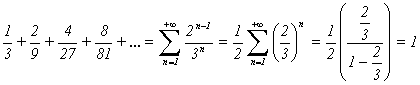
No entanto, podemos afirmar que o conjunto ternário de Cantor C é não vazio, porque os pontos extremos dos intervalos retirados, como 1/3, 2/3, 1/9, 2/9, 7/9, 8/9, lhe pertencem. Além disso, o conjunto ternário de Cantor é um subconjunto compacto de IR, por ser intersecção de intervalos fechados e limitados.
O conjunto de Cantor é um fractal, porque a sua dimensão topológica = zero é menor que a sua dimensão fractal
