Teresa Dias
Departamento de Matemática
A CURVA DE KOCH
Vejamos outra construção idêntica à do conjunto ternário de Cantor no plano, mas neste caso adicionando conjuntos em vez de os remover. Consideremos três segmentos de recta, que constituem os lados de um triângulo equilátero K0 de lado 1
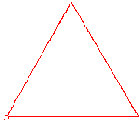
e substituamos o terço médio de cada lado por um triângulo equilátero, do qual lhe suprimimos a base, como indica a figura:

Obtemos um polígono K1 estrelado com 12 lados. A 2ª etapa da construção consiste em repetir o processo anterior, em cada um dos 12 lados do polígono K1, obtendo-se o polígono K2 com 48 lados de comprimento
![]()
K2
Na n-ésima etapa obtemos um polígono Kn com 3.4n-1 lados de comprimento
![]()
Repetindo infinitas vezes este processo, obtemos um subconjunto de IR 2 que se designa por curva de Von Koch.
K3  K4
K4 
Note-se que a área da figura cujo bordo é a curva de Von Koch é positiva (porque é maior que a de K0) e finita (porque é menor que a do quadrado da figura seguinte).

A área de cada triângulo adicionado na construção da curva de Von Koch é 1/9 da área do triângulo adicionado na etapa anterior; e o número de triângulos adicionados é 4 vezes o número de triângulos adicionados, na etapa anterior.
Assim, a área da figura cujo bordo é a curva de Von Koch, que se obtém de K0, é
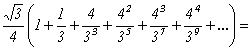
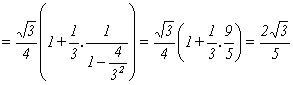
No entanto, o comprimento da curva de Von Koch, embora sendo a fronteira de uma região limitada, é infinito. De facto, como o perímetro do triângulo equilátero K0 é igual a 3, então o perímetro do polígono K1 é
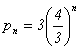
do polígono K2 é
p1= 3 (4/3)1
do polígono K3 é
p2= 3 (4/3)2
e, em geral, o perímetro do polígono Kn é
![]()
Então
![]()
o que permite concluir que o comprimento da curva de Von Koch é infinito.
A curva de Von Koch é um fractal, porque a sua dimensão topológica = 1 é menor que a dimensão fractal
![]()