Inequações de primeiro grau

Introdução

   As inequações do 1º grau com uma variável podem ser escritas numa das seguintes formas:

, , , , como  a e b reais . Exemplos:

Representação gráfica de uma inequação do 1º grau com duas variáveis

Método prático

• Substituímos a desigualdade por uma igualdade.

• Traçamos a reta no plano cartesiano.

• Escolhemos um ponto auxiliar, de preferência o ponto (0, 0) e verificamos se o mesmo satisfaz ou não a desigualdade inicial.

          Em caso positivo, a solução da inequação corresponde ao semiplano ao qual pertence o ponto

          auxiliar.

          Em caso negativo, a solução da inequação corresponde ao semiplano oposto aquele ao qual pertence

          o ponto auxiliar. Exemplos:

• Representa graficamente a inequação

•  

Tabela x y (x, y) 0 4 (0, 4) 2 0 (2, 0)

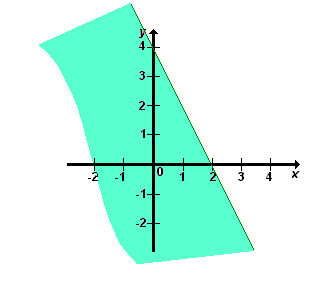   Substituindo o ponto auxiliar (0, 0) na inequação

Inequações de primeiro grau
   

Resolução Gráfica de um Sistema de Inequações do 1º grau

   Para resolver um sistema de inequações do 1º grau graficamente, devemos:

• traçar num mesmo plano o gráfico de cada inequação;

• determinar a região correspondente à intersecção dos dois semiplanos. Exemplos:

• Dê a resolução gráfica do sistema:

        Solução

        Traçando as rectas -x +  y = 4 e 3x + 2y = 6.

    Verificamos:

                                                                                        (Afirmativa positiva, o ponto auxiliar satisfaz a inequação)

   A solução da inequação corresponde ao semiplano ao qual pertence o ponto auxiliar (0, 0).