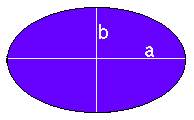
Para calcular a área da região eliptica com semi-eixos a e b entrar com essas medidas nas caixas apropriadas e clicar no botão ÁREA. Tomar a=b para obter a área do Círculo. Com a=b=1 obtemos o valor de pi com 16 decimais exatos.
| Francisco Martins | Cálculo On Line | |
|---|---|---|
|
Número de dias entre duas datas Volume de um sólido elipsoidal |
Número Decimal --> Número Romano | |
Número de dias entre duas datas
|
Inserir as datas e clicar em um
dos 3 botões disponíveis. Você poderá obter o número de dias que já viveu
ou o número de dias entre a data do vencimento da duplicata e a data na
qual você pretende pagá-la. |
|---|
 |
Para calcular a área da região eliptica com semi-eixos a e b entrar com essas medidas nas caixas apropriadas e clicar no botão ÁREA. Tomar a=b para obter a área do Círculo. Com a=b=1 obtemos o valor de pi com 16 decimais exatos. |
Volume de um sólido elipsoidal
Área de um quadrilátero convexo
Um quadrilátero convexo é um polígono convexo que tem quatro lados e os quatro ângulos internos são positivos, tal que a soma dos ângulos alfa, beta, gama e delta vale 360o.
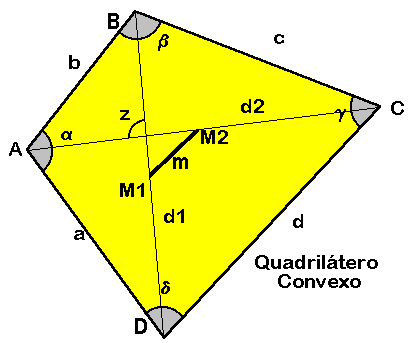
No desenho existem duas diagonais AC e BD de comprimentos respectivamente iguais a d1 e d2. Observa-se também que estas diagonais formam um ângulo z.
Para obter a área do quadrilátero multiplicamos as medidas das diagonais d1 e d2 pela metade do seno do ângulo z, isto é:
Área = (1/2).d1.d2.sen(z)
Logo abaixo apresentamos um "transferidor" para que você possa obter os valores aproximados dos ângulos entre as suas diagonais.
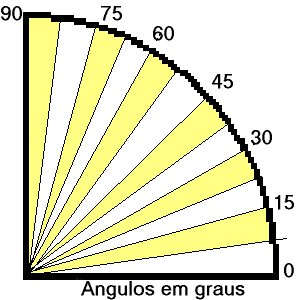
Se o ângulo z possui uma medida próxima de 90o, um valor aproximado para a área é dado pela metade do produto das medidas das diagonais d1 e d2, isto é: A = d1.d2 / 2
Curiosidade: Se a, b, c e d são os lados do quadrilátero convexo, M2 é o ponto médio do segmento AC, M1 é o ponto médio do segmento BD e m é a distância entre M1 e M2, então é verdadeira uma interessante relação matemática:
a2 + b2 + c2 + d2 = d12 + d22 + 4 m2
Cálculo da área do quadrilátero
Para calcular a área do quadrilátero, entrar com as medidas das diagonais
d1 e d2 e o ângulo Ang em graus, nas caixas apropriadas e
clicar no botão Área Quadrilateral.
Se
necessário, use o "transferidor" que está neste trabalho).
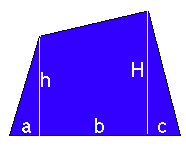 |
Para calcular a área do trapezóide com as dimensões indicadas na figura ao lado, entrar com as medidas nas caixas apropriadas e clicar no botão ÁREA. |
|
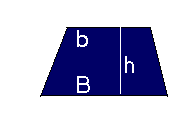
Para calcular a área do trapézio com a base maior B, base menor b e altura h, entrar com as medidas nas caixas apropriadas e clicar no botão ÁREA DO TRAPÉZIO. |
 |