Escoamentos com superfície livre - Ficha resolvida
Exercício 1
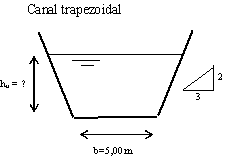
Considere um canal trapezoidal, revestido de betão liso ( K = 75 m1/3s-1 ), com taludes a 2/3 ( V/H) e 5,0 m de largura de rasto.
a) Calcule as alturas do escoamento uniforme para um caudal de 25 m3/s e declives de fundo de 0,01 e 0,0002.
b) Determine as seguintes grandezas:
* altura crítica
* velocidade crítica
* energia específica crítica
* declive crítico
c) Classifique os escoamentos uniformes obtidos.
d) Calcule a altura do escoamento uniforme supondo que o rasto do canal é de terra irregular com vegetação rasteira e que o caudal e o declive do canal são, respectivamente, 25 m3/s e 0,0002.
e) Determine a altura conjugada da altura de regime uniforme no canal para o declive de 0,01.
Resolução
Betão Þ K = 75 m1/3s-1
g = 9,81 ms-2

a) * Q = 25 m3s-1 i = 0,01
|
ITERAÇÃO |
hu |
hun+1 |
|
1 |
1,00 |
0,74942 |
|
2 |
0,74942 |
0,76090 |
|
3 |
0,76090 |
0,76039 |
|
4 |
0,76039 |
0,76041 |
|
5 |
0,76041 |
0,76041 |
Conclusão:
hu = 0,76041 » 0,760 m
* Q = 25 m3s-1 i = 0,0002
|
ITERAÇÃO |
hu |
hun+1 |
|
1 |
1,00 |
2,42351 |
|
2 |
2,42351 |
2,19947 |
|
3 |
2,19947 |
2,23370 |
|
4 |
2,23370 |
2,22842 |
|
5 |
2,22842 |
2,22922 |
|
6 |
2,22922 |
2,22910 |
|
7 |
2,22910 |
2,22913 |
|
8 |
2,22913 |
2,22912 |
|
9 |
2,22912 |
2,22912 |
Conclusão:
hu = 2,22912 » 2,229 m
b) * Altura Crítica
|
ITERAÇÃO |
hc |
hcn+1 |
|
1 |
0,00 |
1,36592 |
|
2 |
1,36592 |
1,18285 |
|
3 |
1,18285 |
1,20551 |
|
4 |
1,20551 |
1,20267 |
|
5 |
1,20267 |
1,20302 |
|
6 |
1,20302 |
1,20298 |
|
7 |
1,20298 |
1,20298 |
Conclusão:
hc = 1,20298 » 1,203 m
* Velocidade crítica
= 3,05412 » 3,054 ms-1
* Energia específica crítica
= 1,67840 » 1,678 m
* Declive crítico
= 1,976 *10-3 m/m
ic=0,001976
c) Classificação dos escoamentos uniformes:
Se: hu > hc Þ Regime lento
hu < hc Þ Regime rápido
* Declive do fundo igual a 0,01
hu = 0,760 m
hc = 1,203 m
Como hu < hc Þ Escoamento uniforme em regime rápido
d) Calculo da altura de escoamento uniforme sendo o rasto do canal de terra irregular com vegetação rasteira .
Q = 25 m3s-1 i = 0,0002
Terra irregular com vegetação rasteira Þ K = 35 m1/3s-1 (Quintela pag. 254)
Paredes laterais em betão liso Þ K = 35 m1/3s-1
|
ITERAÇÃO |
hu |
Kn+1 |
hun+1 |
|
1 |
1,00 |
43,78890 |
3,34684 |
|
2 |
3,34684 |
54,23926 |
2,51103 |
|
3 |
2,51103 |
51,44548 |
2,74116 |
|
4 |
2,74116 |
52,28819 |
2,67234 |
|
5 |
2,67234 |
52,04269 |
2,69224 |
|
6 |
2,69224 |
52,11495 |
2,68653 |
|
7 |
2,68653 |
52,09374 |
2,68827 |
|
8 |
2,68827 |
52,09997 |
2,68776 |
|
9 |
2,68776 |
52,09814 |
2,68791 |
|
10 |
2,68791 |
52,09804 |
2,68786 |
|
11 |
2,68786 |
52,09852 |
2,68787 |
|
12 |
2,68787 |
52,09857 |
2,68787 |
Conclusão:
K = 52,0985 » 52,10
hu = 2,68787 » 2,688 m
e) Altura conjugada para o canal com i = 0,01
Para i = 0,01 temos um escoamento uniforme em regime rápido Û h1 = 0,760 m
(h1 foi calculado na alínea anterior)
![]()
![]()
![]()
Resolvendo a equação anterior iterativamente temos;
h2 = 1,55013 » 1,55 m
Conclusão: A altura conjugada da altura de regime uniforme no canal para o declive de 0,01é de 1,55 m.
Exercício 2
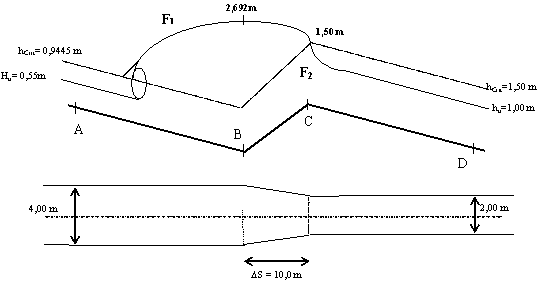
O canal representado na figura transporta o caudal de 11,5 m3s-1 e contém a transição BC, na qual o canal estreita de 4,00 m para 2,00 m, ao longo de 10,0 m. Para esse caudal as alturas uniformes nos trechos AB e CD, com o mesmo declive, são respectivamente 0,55 m e 1,00 m.
Determine:
a) As alturas de água em B e C, para uma descida do fundo, entre essas secções de 0,50m.
b) As alturas de água em B e C, para uma descida do fundo, entre aquelas secções, de 0,50 m .Trace qualitativamente o perfil a superfície livre para os casos das alíneas a) e b).
Na resolução do problema despreze as perdas de carga na transição.

Resolução
a) Considerando o canal com secção rectangular e uma subida do fundo do canal de Dy= 0,50 m, teremos a seguinte expressão para o calculo da altura crítica:
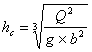
Para;
b = 4,00 m Þ hc = 0,9445 m hu < hc Þ Escoamento em regime rápido
b = 2,00 m Þ hc = 1,4993 m hu < hc Þ Escoamento em regime rápido
huAB = 0,55 m
huCD = 1,00 m
* Vamos considerando, por hipótese que temos em B um escoamento uniforme em regime rápido.
- Cálculo da energia na secção B (Sendo q = Q/b)
![]()
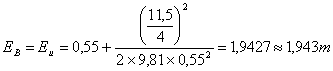
- Cálculo da energia na secção C
EC = EB- Dy = 1,94 - 0,50 = 1,44 m
- Cálculo das altura críticas nas secções B e C
ECrit B = 3/2 hCrit B = 3/2 * 0,9445 = 1,41675 » 1,42 m
ECrit C = 3/2 hCrit C = 3/2 * 1,5 = 2,25 m
Conclusão: EC < ECrit C
Nestas condições, o escoamento não pode chegar à secção B em regime rápido, ou seja as condições a montante de B têm de se modificar, por forma a que o escoamento atinja C com a energia específica mínima, ECrit (energia crítica) ou em regime crítico.
Então na secção B a energia específica será;
E B = ECrit C + Dy = 2,25 + 0,50 = 2,75 m
Sendo, então na secção B o escoamento em regime lento com hu tal que:
![]()
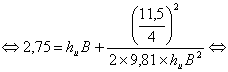
hu B = 2,69182 » 2,692m
Conclusão: A altura de água em B é 2,692 m
A altura de água em C é 1,50 m
Traçado qualitativo do perfil da superfície livre:
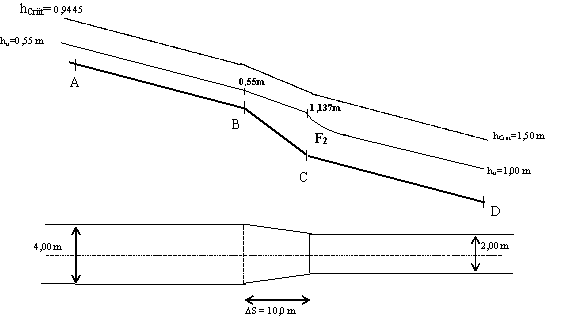
b) Considerando o canal com secção rectangular e uma descida do fundo do canal de Dy= 0,50 m.
A altura de água na secção B será hu = 0,55 m, uma vez que o escoamento uniforme é em regime rápido ( hu < hcrit no troço AB ).
A energia na secção B é EB = 1,94 m ( determinada na alínea anterior )
Cálculo da energia na secção C:
EC = EB+ Dy = 1,94 -+ 0,50 = 2,44 m
Como EC > ECrit C , confirma a hipótese adoptada, assim teremos;
![]()
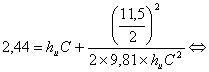
hu C = 1,13734 » 1,137 m
Traçado qualitativo do perfil da superfície livre:
Exercício 3
O canal AC, de betão liso (K = 75 m1/3s-1 ), tem secção rectangular, de 3,0 m de largura, e transporta o caudal de 10 m3/s.
Na secção B o canal tem instalada uma comporta com um coeficiente de contracção de 0,60.
O troço de jusante é suficientemente comprido para que nele se estabeleça praticamente o regime uniforme.
Determine:
a) a altura de água em C
b) a maior abertura da comporta compatível com a existência de um ressalto livre a jusante.
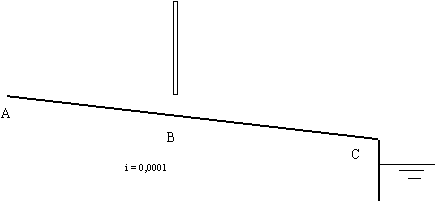
a) Altura de água em C
Q = 10 m3s-1 K = 75 m1/3s-1 CC = 0,60 b = 3,00 m
* Determinação da altura crítica do escoamento, hC
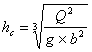 hC=
1,0424 »
1,042 m
hC=
1,0424 »
1,042 m
* Determinação da inclinação crítica, iC
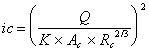
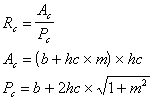
AC = 3,26 m2
PC = 5,084 m
Rh = 0,61487
iC = 3,48*10-3 » 0,0035
i < iC Þ Escoamento uniforme em regime lento
Conclusão:
Como o escoamento uniforme se dá em regime lento a altura de água em C é igual à altura crítica ou seja 1,042m
b) A maior abertura da comporta compatível com a existência de um ressalto livre a jusante.
Ressalto livre a jusante Þ altura da secção contraída seja menor que a altura conjugada em regime lento.
h S C < h2
* Calculo da altura do escoamento uniforme em regime lento
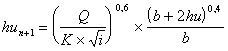
|
ITERAÇÃO |
hu |
hun+1 |
|
1 |
1,00 |
3,002135 |
|
2 |
3,002135 |
3,798580 |
|
3 |
3,798580 |
4,054318 |
|
4 |
4,054318 |
4,131486 |
|
5 |
4,131486 |
4,154351 |
|
6 |
4,154351 |
4,161090 |
|
7 |
4,161090 |
4,163073 |
|
8 |
4,163073 |
4,163656 |
|
9 |
4,163656 |
4,163828 |
|
10 |
4,163828 |
4,163878 |
|
11 |
4,163878 |
4,163893 |
|
12 |
4,163893 |
4,163894 |
Conclusão:
hu = h2= 4,16389» 4,164 m
Altura conjugada de h2:
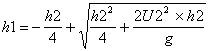
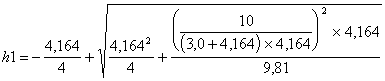
h1 = 0,12679 » 0,127 m
h S C = CC * abertura ( a )
h S C < 0,127 Û 0,60 * a < 0,127 Û
a < 0, 21 m
Conclusão:
A maior abertura da comporta compatível com a existência de um ressalto livre a jusante é de 0,21 m.
Traçado qualitativo do perfil da superfície livre:
