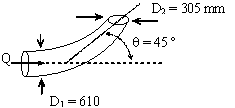
Desprezando as perdas de carga entre as secções 1 e 2, calcular a força exercida na curva de redução a seguir indicada , sabendo que o caudal de água escoado é de 400 l/s e que a pressão na secção 1 é de 1,5 Kgf/cm2. Os diâmetros são respectivamente 610 mm e 305mm.
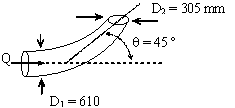
Determine a força exercida na curva a 90 graus indicada na figura, considerando que no percurso se dá uma perda de carga de 1,0 m e que o caudal escoado, de um líquido de peso específico 850 Kgf/m3, é de 890 l/s. Considere que o diâmetro é constante e que a pressão na secção 1 é de 3 Kgf/cm2 (considere que a curva é plana).
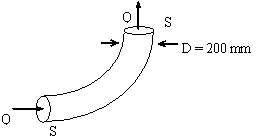
Um jacto de diâmetro 76,2 mm animado de uma velocidade de 33,5 m/s, choca com uma lâmina que se move na mesma direcção com uma velocidade de 21,35 m/s, sendo essa placa curva fazendo um angulo de 150 º com a direcção do jacto. Determinar a força do jacto sobre a superfície.
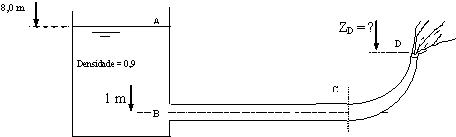
O reservatório representado na figura alimenta uma conduta BC de diâmetro 0,5m e de eixo horizontal à cota de 1 m, à qual se segue a curva CD a 90º terminada pelo orifício D com um diâmetro de 0,25 m. O caudal escoado é de 0,50 m3s-1, verificando-se uma perda de potência no escoamento de 4410 W entre as secções B e C sendo nulas as restantes perdas. Determine a cota do orifício D e a força na curva CD em grandeza, direcção e sentido, desprezando o peso do líquido nela contido. ( Considere g = 9,8 m s-2 )