Cálculo da área da região limitada pela cardióide e cálculo do seu comprimento
1- Área
Consideremos as seguintes funções que representam cardióides e cujos gráficos são: (ver gráficos)> card1:=t->a*(1-cos(t));
![]()
> card2:=t->a*(1+cos(t));
![]()
> card3:=t->a*(1-sin(t));
![]()
> card4:=t->a*(1+sin(t));
![]()
Pretendemos determinar uma expressão geral para a área da região plana limitada por cada uma das curvas anteriores.
Suponhamos que a>0
A área da região plana
limitada por uma curva r = p(t) , em coordenadas polares,
e pelas semi-rectas t = t1 e t =t
é dada por Área =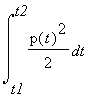
> assume(a>0):
> área1:=int(1/2*(card1(t))^2,t=0..2*Pi);
![]()
> área2:=int(1/2*(card2(t))^2,t=0..2*Pi);
![]()
> área3:=int(1/2*(card3(t))^2,t=0..2*Pi);
![]()
> área:=int(1/2*(card4(t))^2,t=0..2*Pi);
![]()
Podemos concluir que a área de uma cardióide é dada por
Área=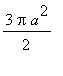
2- Comprimento
O Comprimento de uma curva r = p(t) em coordenadas polares entre t = t1 e t =t é dado por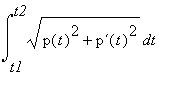
No caso da cardióide, vejamos a que é igual o comprimento.
> comp1:=int(sqrt((card1(t))^2+(D(card1)(t))^2),t=0..2*Pi);
![]()
> comp2:=int(sqrt((card2(t))^2+(D(card2)(t))^2),t=0..2*Pi);
![]()
> comp3:=int(sqrt((card3(t))^2+(D(card3)(t))^2),t=0..2*Pi);
![]()
> comp4:=int(sqrt((card4(t))^2+(D(card4)(t))^2),t=0..2*Pi);
![]()
Podemos concluir que o comprimento
de uma cardióide é sempre igual a 8a.