Prova de que a curva de Durer é um Caracol de Pascal
Uma equação polar do caracol de pascal é r = k + 2a costConsideremos a figura obtida na definição e coloquemos um sistema de eixos como se indica
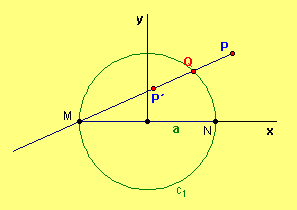
Figura 1
x = r cost -a = k cost + 2r cos2t- a = k cost + a cos2t
y = r sent = k sent + 2a cos t sent= k sent + a sen2t
Considere-se agora a figura 2 que corresponde a uma simplificação da construção de Dürer, considerando o sistema de coordenadas OXY.
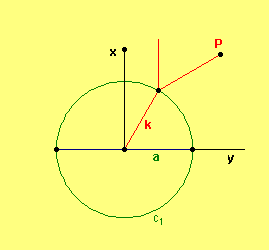
Figura 2
Repare-se que se o raio da circunferência for k e o segmento que se acrescenta tiver comprimento a , a partir da figura, vemos que as coordenadas do ponto são:
x = k cost + acos2t
y = k senq + a sen2t
Podemos então concluir que a curva que
Dürer construiu era de facto a curva que mais tarde se veio a chamar
Caracol de Pascal.