A Cardióide - Projecto de UCEM
Paula Cristina Vaz Pestana
Mestrado em Ensino da Matemática - Departamento de Matemática Pura
Faculdade de Ciências - Universidade do Porto
CARDIÓIDE CURIOSIDADES GLOSSÁRIO LINKS
Definições e Construções
Caracol de Pascal
Equações Polares
Como Epiciclóide
 Área e Comprimento
Superfície de Revolução
Coração Animado
Mecanismos
Curva Cáustica
   
 

Caracol (Limaçon) de Pascal

Nota Histórica

O nome Caracol de Pascal foi atribuído a esta curva por Roverbal (por volta de 1730) que a utilizou para desenhar tangentes a curvas e mais tarde calculou a sua área. Esta curva foi estudada por Étienne Pascal, pai do matemático e filósofo Blaise Pascal.
Ao longo dos tempos foram publicados diversos artigos onde se expuseram as propriedades do caracol e diversas formas de o construir.
Foram também inventados aparelhos para descrever mecanicamente esta curva através de um movimento contínuo.
O primeiro destes mecanismos foi construído por Peaucellier e é constituído por duas barras articuladas e deu-o a conhecer em 1873 em Nouvelles Annales de Mathématiques.

 Definições

Tal como  no estudo da cardióide  é possível definir esta curva de diversas formas e ,com a ajuda do software dinâmico Geometer´s Skhetchpad,  construir a curva a partir de cada uma das definições. 

Façamos a construção a partir das seguintes definições:

Definição 1
Definição 2
Método de Dürer

Definição 1- Consideremos uma circunferência c1de raio a e diâmetro MN. Consideremos um ponto Q sobre c1  e a recta q definida por M e Q.
Seja dado um número k<2a e marquemos sobre q dois pontos P e P´, distando k do ponto Q.
Se imaginarmos o ponto Q a deslocar-se sobre c1 , o lugar geométrico dos pontos P e P´ é o caracol de Pascal.

Nota: Se k = 2a, obtemos a cardióide.

Na figura seguinte poderá ver uma construção dinâmica construída no programa dinâmico Geometer´s Sketchpad, tendo por base esta definição
 
 
Esta página necessita de um browser compatível com JAVA.
Figura 1
 
 
 

Observações:
-O comprimento do segmento AB é a.
- O comprimento do segmento CE é 2a
- O comprimento de CD é k.
-verifique que se o ponto D coincidir com o ponto E,k =2a e obtém-se a cardióide

Definição 2- Caracol como curva pedal da circunferência
Considere-se uma circunferência c e um ponto Q no exterior.
O lugar geométrico dos pés das perpendiculares T traçados por P às tangentes a c é um Caracol de Pascal.

Observe-se a construção.
 
Esta Página necessita de um browser compatível com JAVA.
Figura 2
 
 
 
 
 
 
 
 
 

Observações:
-Verifique-se que se se fizer coincidir o ponto Q´com o ponto Q  se obtém uma cardióide.

 

EQUAÇÃO DO CARACOL DE PASCAL 

Coordenadas polares

Tendo em conta a definição 1 e sendo t o ângulo PMN  e r o comprimento do segmento MP  deduz-se, de modo análogo ao que foi feito para a cardióide, a seguinte equação do Caracol de Pascal em coordenadas polares
       r = k + 2a cost

Note-se que para k = 2a obtém-se a equação da cardióide que já deduzimos. Há uma diferença de sinal que resulta do facto de as curvas estarem dispostas de modo simétrico em relação ao eixo OY.
 

MÉTODO DE DÜRER 

A seguir apresenta-se um método de construção do caracol que preza pela originalidade. 
Dürer, que viveu um século antes de Pascal já conhecia o caracol, mas não lhe deu esse nome. O método por ele utilizado é bastante original e consiste numa construção por pontos do seguinte modo:

1- Traça-se uma circunferência que se divide em 12 arcos iguais, numerando-se os pontos de divisão como se fossem as horas de um relógio.
2- A partir das extremidades dos raios 1,2,3,4... são traçados segmentos , todos iguais, paralelos aos raios 2,4,6,8... respectivamente
3- Unem-se as extremidades destes segmentos por uma curva
4- A curva obtida será um caracol de Pascal se a divisão da circunferência em arcos for cada vez maior.

Na figura seguinte  apresenta-se a construção descrita

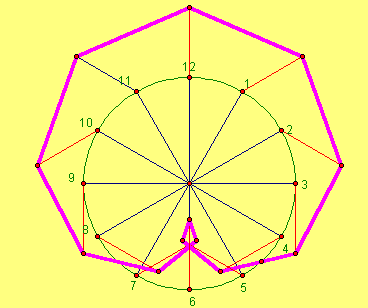
Figura 3

Mas como poderemos  ter a certeza que, de facto, a curva construída deste modo  é um caracol de Pascal? 
Se tiver curiosidade poderá ver a seguinte prova.